热斑效应和阴影遮挡对分布式电站的影响分析

 分布式电站不同于大型地面电站，分布式电站一般建设在工商业企业的屋顶上。大部分工商业屋顶也会摆放其他设备。例如：中央空调的冷却塔、普通空调的压缩机、电梯井。同时周围高大建筑物和树木都会在特定时刻产生影响屋顶分布式电站的阴影；树叶和鸟粪会在电池组件的表面附着。空调系统会造成发电系统局部阵列升温。 由于上述复杂因素，必须对这些因素对发电系统的影响进行分析。

1.1热斑效应和数学模型

热斑效应是指正常工作的电池组件在某一时刻，一个单体电池片被小的物体遮盖。导致此单体电池所能产生的电流变小。电池组件中的单体电池片可以看成是一个具有类似二极管的P-N结结构，具有反向雪崩击穿现象，根据基尔霍夫电流与电压定律，当被遮挡的单体电池所能产生的电流小于电路的电流时，该单体电池带负压，成为负载。并以发热形式消耗其他单体电池片发出的能量。
式（1-1）所示在电池组件正常工作时，光生电流IPH 被3个环节消耗了，一部分被负载消耗（I），一部分被内阻消耗了（Ipa+Ise），一部分被等效二极管消耗掉了（Id）当出现热斑现象时，Ipa、Ise、 Id数值会变大，三者叠加到达一定值时，单体电池片会被击穿。热斑效应跟电池组件的生产工艺也有很大关系。由于生产水平的缺陷，往往会导致单体电池片的内阻不均匀。内阻不均匀的电池片极易产生热斑现象。

热斑效应的危害非常大。轻则烧毁电池片，严重的会引起整片电池组件的燃烧并引起火灾。近几年由热斑效应引起的电站火灾多有发生。分布式电站起火不但会导致财产损失，严重的会造成人员伤亡。这就要求电站管理方定期巡检及时清洁，避免危险产生。
1.2环境因素对电池组件的影响

1.2.1 STC标准测试条件 

STC（Standard Test Condition）测试是一种标准测试。基本原理是当闪光照到被测电池上时，用电子负载控制太阳电池中电流变化，测出电池的伏安特性曲线上的电压和电流，温度，光的辐射强度，测试数据送入微机进行处理并显示。国际同行标准的测试环境：辐照度1000W/M2，环境温度25 °C, AM=1.5；功率公差范围： ± 3%. 图1-4所示，某厂家型号为ET-M672280WW 280Wp电池组件在STC环境下的P-U曲线。（本章都以此型号电池组件为实验及仿真对象）
1.2.2 遮挡对电池组件的影响

云层、高大建筑和树木产生的大面积阴影对电池组件的直接影响就是太阳能辐照度的变化。图1-4中曲线是在辐照度1000W/ M2条件下生成的，图1-5生成了5种不同辐照度条件的P-U曲线和最大功率点数据。见表1-1
由表1-1中数据所示，辐照度越大组件的输出功率越大，反之越小。 

1.2.3 温度对电池组件的影响 

太阳能电池组件有2个和温度有关的参数即电压温度系数、电流温度系数。ET-M672280WW电池组件的开路电压温度系数为-0.33%/K。即当温度每升高一开尔文，组件的开路电压会下降0.33%，约146mV，反之上升。 电池组件的短路电流温度系数为0.031%/K。当温度每升高一开尔文，组件的短路电流会上升0.031%，约2.49mV，反之下降。 温度上升导致的电压和电流的变化，由于电流的变化幅度较小。图1-6所示，温度对组件的功率还是有比较大的影响，温度每上升一个开尔文，电池组件的输出功率下降0.39%
约1.1W。图1-7生成数据，温度每10K上升一次功率下降10-11W.
由此可见，温度对发电系统的影响较大。在电站设计选址时，应该避免靠近空调压缩机。并适当增大电池组件之间以及组件和地表的距离，达到通风散热的目的。

1.3 标准太阳能组件数学建模以及MATLAB仿真
1.3.1 数学模型
式（1-2）为标准的电池组件数学模型，光生电流等于流过负载的电流、反向饱和电流、流过内阻电流三者之和。（参数见表1-2）

式（1-2）是一个含有多个未知量的超越方程，式中电池的串联、并联内阻、二极管的品质因子、光生电流、二极管的反向包和电流都不方便测量。为了方便工程应用和工程建模。
忽略了并联电阻的数据，因为并联电阻太大往往有150-300欧姆。式（1-2）可以改写为式（1-3）

当电池在开路状态下，I=0;V=Voc；在最大功率点状态下，I=Impp；V=Vmpp；设Iph=Isc
可得式 （1-4）（ 1-5）

由于在25℃下EXP[Vmpp/(C2Voc)] >>1可以忽略式中的“-1”项从而解出C1:

组件开路状态下，I=0;V=Voc；并把（1-6）带入（1-4）得：解出C2：
1.3.2 MATLAB工程建模 
由式（1-3）-（1-12）进行MATLAB工程建模后，电池组件的内部关联如 图1-8 
将内部关联结构封装后进行参数设定，图1-9所示。组件的开路电压、短路电流
最佳工作电压、电流，电压、电流温度系数，温度，太阳能辐照度等参数都可以自
由设定。
图1-10是MATLAB模型通过仿真后，得到的STC条件下的U-I曲线；图1-11是辐照度800W/ M2、温度45摄氏度条件下MATLAB模型生成的P-U曲线；图1-12是辐照度800W/ M2、温度45摄氏度条件下Pvsyst软件生成的P-U曲线。图1-13是在MPPT下的P-T仿真图。（扰动观测法）
由图可见MATLAB和Pvsyst软件仿真的数据有1-2%的差距，说明通过数学模型推导出来的MATLAB电池组件模型完全可以用于工程仿真。

1.4 复杂环境下的分布式电站MATLAB仿真 

大多数分布式电站受到屋顶面积的限制,装机容量都不大。同时受到配电室面积的制约也没有办法使用体积庞大的集中式逆变器。通常会使用户外式的多路MPPT组串式逆变器。目前组串逆变器的功率在10KW-50KW之间，可以根据电站装机容量的大小灵活配置。
图1-14所示为光伏阵列的等效电路，每一块电池组件都并联了一个旁路二极管。如果组件被遮挡，二极管导通。被遮挡的组件会被旁路，从而不影响其他电池组件的工作。如果使用集中式逆变器,直流电流经过汇流箱、直流配电柜汇集到逆变器的直流侧。按照常规设计，每一台500Kw集中式逆变器会并联112串电池组串，每个组串会由18-20块电池组件串联。由于组件之间的个体差异造成组串之间的电压和电流的差异,又因为并联的组串数量过多，这就造成了不同大小电压的耦合，降低了整个光伏阵列的效率。

对于大型地面站如果没有严重的遮挡，仅仅因为电压不匹配的造成的功率损失很少。但是对于分布式电站来说，如果环境复杂，就不适合使用集中式逆变器。应该使用带多路MPPT的组串式逆变器。

组串式逆变器有2-3个MPPT，这样可以把由于遮挡或者组件个差异造成的电压差异解耦(图1-16)。这样就做到了被遮挡组件和正常工作组件的互不影响，功率得到充分的利用。由于组串逆变器的这一特点，本小节只研究一个组串被遮挡的情况。


1.4.1被遮挡的组件的数学模型
一个N块组件组成的组串的模型。仍可由式1-2、1-3 表示。图1-15所示2块串联的组件的等效电路图。

（1）一块组件对外输出功率时  
在有遮挡的情况下，假设IPH1≠IPH2 随着外接负载的不同，旁路二极管有导通或者阻断2种情况发生。当外接负载电阻很小，组件输出电流很大时，假设IPH1＞IPH2，组件1的输出电流大于组件2产生的电流IPH2。组件2的旁路二极管导通．组件1多余的电流从旁路二极管流过对外输出．只有组件1对外输出功率，组件2吸组件1输出的一部分功率，因此串联后的电流方程就是组件1的输出特性方程。见式 （1-14）

为旁路二极管的电压降，可以用式（1-15）表示： 

把式(1-15)带入（1-14）得（1-16）

（2）二块组件同时对外输出功率

当外接负载增大时，组件的输出电流减小。被遮挡的组件2产的生的电流可以对外输出功率时候，组件1和组件2同时工作，即 IPH1=IPH2时。此时的特性方程为式（1-17）

综合组件遮挡后输出的两种情况，可以确认组件输出的U-I曲线和P-U曲线不在是单峰特性。
存在2个峰值。特性方程可以用分段函数表示如式（1-18）

1.4.2 MATLAB模型搭建

本章第3节中已经证明了单体组件的matlab模型的实用性。根据式（1-13）-（1-18）
建立模型架构如图1-17
模型其中包含两个组件串联的模型， 模型中的S为光照强度，默认理想情况为1000，T为温度默认为25℃。局部阴影情况仿真时改变一定数量光伏电池的光照强度即可实现，2个光伏电池的光照条件和温度可以调节。仿真结束后在matlab主界面输入plot(Udc,Power)绘制U-P曲线，输入plot(Udc,Ipv)绘制U-I曲线。图1-19为实验模型主体，包括示波器、电压、电流表和可调负载。仿真模拟280wp多晶硅组件参数。
仿真1：模拟STC条件下2块280wp组件P-U和U-I曲线。见图1-20,1-21；
仿真2：大电流情况下负载（5Ω），2块280wp有一块组件被遮挡时(500W/M2)P-U和U-I曲线。见图1-21，图1-22.在负载较小的时候，组件的输出电流较大。导致旁路二极管导通，被遮挡的组件被旁路。组件的输出特性没有明显变化，符合数学模型的推导。见图1-22,1-23；

仿真3：小电流情况下负载（50Ω），2块280wp有一块组件被遮挡时(500W/M2)P-U和U-I曲线。见图1-21，图1-22.在负载较大的时候，组件的输出电流较小。旁路二极管没有导通组件的输出特性符合双峰特性，符合数学模型的推导。见图1-24,1-25。双膝、双峰曲线也基本符合FLUKE-IV测试仪器现场测量的曲线。图1-26,1-27
1.4.3 多组件模块复杂环境下MATLAB仿真

如图1-28模拟了10片电池组件（PV、PV1模块各封装了4块组件，PV2封装了2块组件）被复杂物体遮挡。局部温度到达65摄氏度。平均辐照度800 W/M2，局部遮挡后4块电池组件辐照度降低至200 W/M2、1块降低至500 W/M2 。
仿真后得到图1-29、图1-30，由于全局有3个辐照度变量1个温度变量。U-I曲线出现了3个明显的局部膝点。P-U图形出现了3个局部峰值功率点。基本吻合文献【8】中的理论推导。

由仿真结果可以看出全局最大功率为0.88KW，没有遮挡情况下800 W/M2，25℃时10块280Wp的理论最大功率应为2.25KW。计算出的功率损失61%。这一仿真结果符合工程实际情况。

小结：本章首先分析了热斑效应的原理，并从原理角度说明了热斑效应的产生和危害。并指出只有加强巡检才能避免热斑效应。其次推导出了电池组件的工程模型，并验证了工程模型的可靠性。最后推导出了复杂环境下的电池组件数学模型，并进行了MATLAB仿真并得到了符合工程实际的结果。该工程模型可以模拟复杂环境下的组件输出特性。在一些情况下比PVSYST软件更加方便使用。

参考文献：
【1】太阳电池热斑现象和成因的分析 伊纪椽，刘文祥，马洪斌 王晟2(1．中国电子科技集团公司第十八研究所，天津300384；2。海军装备部，北京100841)
【2】刘平．王雩冬太阳电池阴影效应及热斑[J】物理实验．1997．C2)：4243
【3】茆美琴，余世杰，苏建徽. 带有MPPT功能的光伏阵列Matlab通用仿真模型[J].系统仿真学报，Vol.17,No.5,2005
【4】 苏建徽，余世杰，赵 为，等.硅太阳电池工程用数学模型[J].太阳能学报，2001（4）:409-412
【5】被部分遮挡的串联光伏组件输出特性翟载腾，程晓舫，丁金磊，查琚(中国科学技术大学热科学和能源工程系，安徽合肥230027) 中图分类号：TM914．4 文献标识码：A
【6】王长江. 基于MATLAB的光伏电池通用数学模型[J]. 电力科学与工程, Vol.25, No.4,2009
【7】D.Menniti,A.Burgio,N.Sorrentino,A.Pinnarelli, G.Brusco. An Incremental Conductance Method with Variable Step Size for MPPT: Design and Implementation. Electrical Power Quality And Utilization,September 15-17,2009,Lodz,Poland
【8】张　兴，曹仁贤．太阳能光伏并网发电及其逆变控制［M ］ ．
北京：机械工业出版社，２０１１ ：２３９ － ２５１ ．
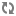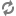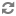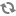